#include "cont_math.h"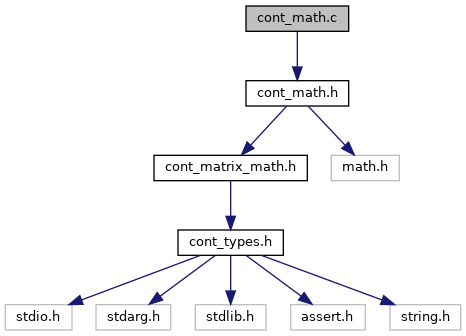
Go to the source code of this file.
Functions | |
| int | cont_SU2_conjugate (matrix_double_t *qin, matrix_double_t *qout) |
| Conjugate an element of SU(2) More... | |
| int | cont_SU2_product (matrix_double_t *q, matrix_double_t *p, matrix_double_t *out) |
| Product of two elements of SU(2) More... | |
| int | cont_SU2_vee (matrix_double_t *in, matrix_double_t *out) |
| The vee map on SU(2) More... | |
| int | cont_SU2_hat (matrix_double_t *in, matrix_double_t *out) |
| The hat map on SU(2) More... | |
| int | cont_SU2_Exp (matrix_double_t *in, matrix_double_t *out) |
| The Exp map on SU(2) More... | |
| int | cont_SU2_triple (double a, double b, double c, matrix_double_t *out) |
| Computes a triple product on SU(2) More... | |
| double | cont_SU2_distance (matrix_double_t *q1, matrix_double_t *q2) |
| Evaluate distance Gamma(q1, q2) in [0,2] defined on SU2. More... | |
| int | cont_quat_2_SO3 (matrix_double_t *q, matrix_double_t *R) |
| Embedding relating SU(2) to SO(3) More... | |
| int | cont_SO3_hat (matrix_double_t *in, matrix_double_t *out) |
| The hat operator on SO3. More... | |
| int | cont_SO3_vee (matrix_double_t *in, matrix_double_t *out) |
| The hat operator on SO3. More... | |
| int | cont_SO3_Exp (matrix_double_t *in, matrix_double_t *out) |
| The Exp map on SO3. More... | |
| int | cont_SO3_Log (matrix_double_t *in, matrix_double_t *out) |
| The Log map on SO3. More... | |
| double | cont_SO3_distance (matrix_double_t *R1, matrix_double_t *R2) |
| The distance Phi(R1, R2) defined on SO3. More... | |
| double | cont_sinc (double x) |
| Evaluates the sinc function as f(x) = sin(x)/x. More... | |
| double | cont_dot_product (matrix_double_t *vecA, matrix_double_t *vecB) |
| Evaluates the dot product of two vectors. More... | |
| void | cont_cross_product (matrix_double_t *inAm, matrix_double_t *inBm, matrix_double_t *outm) |
| Cross product operation, To be migrated to the cont_math stack. More... | |
| double | cont_sign_func (double in) |
| Takes the sign of the input, returning +1 if the input is zero. More... | |
| int | cont_normalize (matrix_double_t *vec) |
| Normalizes the vector. More... | |
Function Documentation
◆ cont_cross_product()
| void cont_cross_product | ( | matrix_double_t * | inAm, |
| matrix_double_t * | inBm, | ||
| matrix_double_t * | outm | ||
| ) |
Cross product operation, To be migrated to the cont_math stack.
- Parameters
-
[in] inAm - Input vector A in R^3 [in] inBm - Input vector B in R^3 [out] outm - Output as the cross-product of A and B, out=AxB, in R^3
- Returns
- void
Definition at line 359 of file cont_math.c.
◆ cont_dot_product()
| double cont_dot_product | ( | matrix_double_t * | vecA, |
| matrix_double_t * | vecB | ||
| ) |
Evaluates the dot product of two vectors.
- Parameters
-
[in] vecA - Input vector [in] vecB - Input vector
- Returns
- output - dot product
Definition at line 343 of file cont_math.c.
◆ cont_normalize()
| int cont_normalize | ( | matrix_double_t * | vec | ) |
Normalizes the vector.
- Parameters
-
[out] vec - Input vector with either 1 row, or 1 column
- Returns
- output - 1 if successful, 0 otherwise
Definition at line 378 of file cont_math.c.
◆ cont_quat_2_SO3()
| int cont_quat_2_SO3 | ( | matrix_double_t * | q, |
| matrix_double_t * | R | ||
| ) |
Embedding relating SU(2) to SO(3)
- Parameters
-
[in] q - Pointer to a four-dimensional input quaternion [out] R - Pointer to an output 3x3 rotation matrix
- Returns
- status - 1 if successful, 0 otherwise
Definition at line 157 of file cont_math.c.
◆ cont_sign_func()
| double cont_sign_func | ( | double | in | ) |
Takes the sign of the input, returning +1 if the input is zero.
- Parameters
-
[in] in - Input argument
- Returns
- output - Output sign in {-1.0, 1.0}
Definition at line 370 of file cont_math.c.
◆ cont_sinc()
| double cont_sinc | ( | double | x | ) |
Evaluates the sinc function as f(x) = sin(x)/x.
- Parameters
-
[in] x - the value at which the function is to be evaluated
- Returns
- output - the output of the function f(x)
Definition at line 333 of file cont_math.c.
◆ cont_SO3_distance()
| double cont_SO3_distance | ( | matrix_double_t * | R1, |
| matrix_double_t * | R2 | ||
| ) |
The distance Phi(R1, R2) defined on SO3.
This distance is defined as Phi(R1, R2) = (1/2)Tr(I - R1'*R2) in [0,2]
- Parameters
-
[in] R1 - Pointer to an output 3x3 rotation matrix [in] R2 - Pointer to an output 3x3 rotation matrix
- Returns
- distance - The evaluated distance on SO(3)
Definition at line 302 of file cont_math.c.
◆ cont_SO3_Exp()
| int cont_SO3_Exp | ( | matrix_double_t * | u, |
| matrix_double_t * | R | ||
| ) |
The Exp map on SO3.
- Parameters
-
[in] u - Pointer to a three-dimensional vector (one parameter group) [out] R - Pointer to an output 3x3 rotation matrix
- Returns
- status - 1 if successful, 0 otherwise
Definition at line 224 of file cont_math.c.
◆ cont_SO3_hat()
| int cont_SO3_hat | ( | matrix_double_t * | in, |
| matrix_double_t * | out | ||
| ) |
The hat operator on SO3.
- Parameters
-
[in] in - Pointer to a three-dimensional vector (one parameter group) [out] out - Pointer to an element of the 3x3 lie algebra of SO(3)
- Returns
- status - 1 if successful, 0 otherwise
Definition at line 186 of file cont_math.c.
◆ cont_SO3_Log()
| int cont_SO3_Log | ( | matrix_double_t * | R, |
| matrix_double_t * | u | ||
| ) |
The Log map on SO3.
- Parameters
-
[in] R - Pointer to an output 3x3 rotation matrix [out] u - Pointer to a three-dimensional vector (one parameter group)
- Returns
- status - 1 if successful, 0 otherwise
Definition at line 265 of file cont_math.c.
◆ cont_SO3_vee()
| int cont_SO3_vee | ( | matrix_double_t * | in, |
| matrix_double_t * | out | ||
| ) |
The hat operator on SO3.
- Parameters
-
[in] in - Pointer to an element of the 3x3 lie algebra of SO(3) [out] out - Pointer to a three-dimensional vector (one parameter group)
- Returns
- status - 1 if successful, 0 otherwise
Definition at line 207 of file cont_math.c.
◆ cont_SU2_conjugate()
| int cont_SU2_conjugate | ( | matrix_double_t * | qin, |
| matrix_double_t * | qout | ||
| ) |
Conjugate an element of SU(2)
- Parameters
-
[in] qin - Pointer to a four-dimensional input quaternion [out] qout - Pointer to a four-dimensional output quaternion
- Returns
- status - 1 if successful, 0 otherwise
Definition at line 10 of file cont_math.c.
◆ cont_SU2_distance()
| double cont_SU2_distance | ( | matrix_double_t * | q1, |
| matrix_double_t * | q2 | ||
| ) |
Evaluate distance Gamma(q1, q2) in [0,2] defined on SU2.
This distance is defined as Gamma(X1, X2) = (1/2)Tr(I - X1'*X2) in [0,2]
- Parameters
-
[in] q1 - Pointer to a four-dimensional input quaternion [in] q2 - Pointer to a four-dimensional output quaternion
- Returns
- distance - The evaluated distance on SU2
Definition at line 138 of file cont_math.c.
◆ cont_SU2_Exp()
| int cont_SU2_Exp | ( | matrix_double_t * | in, |
| matrix_double_t * | out | ||
| ) |
The Exp map on SU(2)
- Parameters
-
[in] in - Pointer to a three-dimensional vector (one parameter group) [out] out - Pointer to an element of SU(2) (here a 4-dimenisonal vector)
- Returns
- status - 1 if successful, 0 otherwise
Definition at line 86 of file cont_math.c.
◆ cont_SU2_hat()
| int cont_SU2_hat | ( | matrix_double_t * | in, |
| matrix_double_t * | out | ||
| ) |
The hat map on SU(2)
- Parameters
-
[in] in - Pointer to a three-dimensional output (one parameter group) [out] out - Pointer to an input element of the lie-agbera of SU(2)
- Returns
- status - 1 if successful, 0 otherwise
Definition at line 69 of file cont_math.c.
◆ cont_SU2_product()
| int cont_SU2_product | ( | matrix_double_t * | q, |
| matrix_double_t * | p, | ||
| matrix_double_t * | out | ||
| ) |
Product of two elements of SU(2)
- Parameters
-
[in] q - Pointer to an input element of SU(2) (four-dimensional vector) [in] p - Pointer to an input element of SU(2) (four-dimensional vector) [out] out - Pointer to an output quaternion product (four-dimensional vector)
- Returns
- status - 1 if successful, 0 otherwise
Definition at line 28 of file cont_math.c.
◆ cont_SU2_triple()
| int cont_SU2_triple | ( | double | a, |
| double | b, | ||
| double | c, | ||
| matrix_double_t * | out | ||
| ) |
Computes a triple product on SU(2)
The inputs a, b, and c all represent angles in radians, and the triple product is computed by taking the exponential map with respect to these angles as
qa = Exp([a, 0, 0]) qb = Exp([0, b, 0]) qc = Exp([0, 0, c])
and then computing their consequtive product
out = qa * qb * qc
- Parameters
-
[in] a - Angle in radians [in] b - Angle in radians [in] c - Angle in radians [out] out - Pointer to an element of SU(2) (here a 4-dimenisonal vector)
- Returns
- status - 1 if successful, 0 otherwise
Definition at line 110 of file cont_math.c.
◆ cont_SU2_vee()
| int cont_SU2_vee | ( | matrix_double_t * | in, |
| matrix_double_t * | out | ||
| ) |
The vee map on SU(2)
- Parameters
-
[in] in - Pointer to an input element of the lie-agbera of SU(2) [out] out - Pointer to a three-dimensional output (one parameter group)
- Returns
- status - 1 if successful, 0 otherwise
Definition at line 53 of file cont_math.c.
